问题
解答题
(12分)已知A(1，0)、B(0，－1)、C(－1，2)、D(2，－1)、E(4，2)五个点，抛物线y＝a(x－1)2＋k(a＞0)经过其中的三个点．
(1)求证：C、E两点不可能同时在抛物线y＝a(x－1)2＋k(a＞0)上；
(2)点A在抛物线y＝a(x－1)2＋k(a＞0)上吗？为什么？
(3)求a和k的值．
答案
解：(1)证明：用反证法。假设C(－1，2)和E(4，2)都在抛物线y＝a(x－1)2＋k
(a＞0)上，联立方程 ，
解之得a＝0，k＝2。这与要求的a＞0不符。
∴C、E两点不可能同时在抛物线y＝a(x－1)2＋k(a＞0)上。
(2)点A不在抛物线y＝a(x－1)2＋k(a＞0)上。这是因为如果点A在抛物线上，则k＝0。B(0，－1)在抛物线上，得到a＝－1，D(2，－1)在抛物线上，得到a＝－1，这与已知a＞0不符；而由(1)知，C、E两点不可能同时在抛物线上。
因此点A不在抛物线y＝a(x－1)2＋k(a＞0)上。
(3)综合(1)(2)，分两种情况讨论：
①抛物线y＝a(x－1)2＋k(a＞0)经过B(0，－1)、C(－1，2)、D(2，－1)三个点，
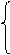a(0－1)2＋k＝－1
联立方程 a(－1－1)2＋k＝2，
a(2－1)2＋k＝－1
解之得a＝1，k＝－2。
②抛物线y＝a(x－1)2＋k(a＞0)经过B(0，－1)、D(2，－1)、E(4，2)三个点，
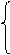a(0－1)2＋k＝－1
联立方程 a(2－1)2＋k＝－1，
a(4－1)2＋k＝2
解之得a＝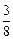
，k＝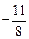
。
因此，抛物线经过B、C、D三个点时，a＝1，k＝－2。抛物线经过B、D、E三个点时，
a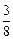＝，k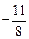＝。