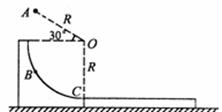
（17分）如图所示，半径R=0.8m的光滑1/4圆弧轨道固定在光滑水平上，轨道上方的A点有一个可视为质点的质量m=1kg的小物块。小物块由静止开始下落后打在圆弧轨道上的B点但未反弹，在该瞬间碰撞过程中，小物块沿半径方向的分速度即刻减为零，而沿切线方向的分速度不变，此后小物块将沿着圆弧轨道滑下。已知A点与轨道的圆心O的连线长也为R，且AO连线与水平方向的夹角为30°，C点为圆弧轨道的末端，紧靠C点有一质量M=3kg的长木板，木板的上表面与圆弧轨道末端的切线相平，小物块与木板间的动摩擦因数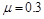
，g取10m/s2。求：
(1)小物块刚到达B点时的速度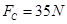
；
(2)小物块沿圆弧轨道到达C点时对轨道压力FC的大小；
(3)木板长度L至少为多大时小物块才不会滑出长木板？
（1）
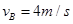，方向竖直向下 （2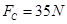）（3）
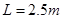
题目分析：（1）由几何关系可知，AB间的距离为R，小物块从A到B做自由落体运动，
根据运动学公式有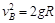 
……(1分)
代入数据解得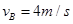， ……… (1分)
方向竖直向下 …………… (1分)
（2）设小物块沿轨道切线方向的分速度为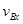
，因OB连线与竖直方向的夹角为
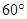，故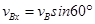
………………(1分)
从B到C，只有重力做功，根据机械能守恒定律有
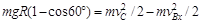…………(2分)
在C点，根据牛顿第二定律有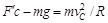
…………(1分)
联立以上各式，代入数据解得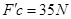
…………(1分)
再根据牛顿第三定律可知小物块到达C点时对轨道的压力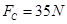 ……… (1分)
（3）小物块滑到长木板上后，小物体做匀减速运动，长木板做匀加速运动
小物体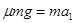 
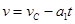(1分)
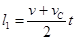(1分)
(1分)
长木板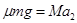 
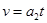(1分)
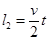(1分)
(1分)
又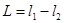 
(1分)
联立以上各式可得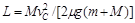 
代入数据解得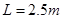 (1分)