问题
计算题
(9分)在游乐场,有一种大型游乐设施跳楼机,如图所示,参加游戏的游客被安全带固定在座椅上,提升到离地最大高度64m处,然后由静止释放,开始下落过程可认为自由落体运动,然后受到一恒定阻力而做匀减速运动,且下落到离地面4m高处速度恰好减为零。已知游客和座椅总质量为1500kg,下落过程中最大速度为20m/s,重力加速度g=10m/s2。求:

(1)游客下落过程的总时间;(2)恒定阻力的大小。
答案
(1)6s;(2)22500N。
题目分析:(1)设下落过程中最大速度为v,自由落体的高度为h1,
则: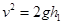 (1分)
(1分) 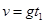 (1分)
(1分)
解得:t1=2s (1分)
设匀减速的高度为h2,加速度大小为a,
则: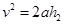
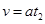
下落的总距离h=h1+h2=64m-4m=60m(1分)
联立解得:a=5m/s2 t2=4s(1分)
游客下落过程的总时间为t=t1+t2=6s (1分)
(2)匀减速过程中:设阻力为f,由牛顿第二定律得:f-mg=ma(2分)
已知m=1500kg,可得f=22500N(1分)
