∵an+2-an+1=an+1-an=a1+1=1(n∈N*)，

∴数列{a_n}是首项为0，公差为1的等差数列

故a_n=n-1

又∵当x∈[n-1，n）时，f（x）=n-3，

当n=1时，x∈[0，1）时，f（x）=-2，

当n=2时，x∈[1，2）时，f（x）=-1，

当n=1时，x∈[2，3）时，f（x）=0，

当n=1时，x∈[3，4）时，f（x）=1，

…

又由方程2^f（x）=x的根

即为f（x）=log₂x的根

在同一坐标系中画出函数y=f（x）和y=log₂x的图象如下图，

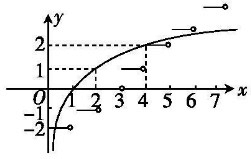
由图可得y=f（x）和y=log₂x的图象有两个交点

故方程2^f（x）=x的根的个数为2个

故选C