问题
填空题
抛物线y=x2-4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积是__
答案
1
物线y=x2-4x+3的顶点及它与x轴的交点三点连线所围成的三角形中:底边长为与x轴的两交点之间的距离,高为抛物线的顶点的纵坐标的绝对值,再利用三角形的面积公式即可求出b的值.
解:由题意可得:抛物线的顶点的纵坐标为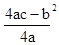 =-1,
=-1,
∴底边上的高为1;
∵x2-4x+3=0,解得x1=1,x2=3,
∴抛物线与x轴的交点为(1,0)、(3,0);
由题意得:底边长=|x1-x2|=2,
∴抛物线y=x2-4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积为:1/2×2×1=1.
