问题
填空题
已知命题“存在x∈R,|x-a|+|x+2|≤2”是假命题,则实数a的取值范围是______.
答案
由绝对值的几何意义可得,|x-a|+|x+2|≤2是指数轴上的数x到数a和数-2的距离之和小于或等于2,由图可得:
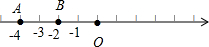
即当数a对应的点位于AO之间时,存在x∈R,|x-a|+|x+2|≤2,
∴-4≤a≤0.
∴“存在x∈R,|x-a|+|x+2|≤2”是假命题,实数a的取值范围是:a<-4或a>0.
故答案为:a<-4或a>0.
