略

设a=cos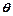,b=sin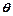,c=cos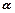,d=sin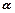        

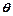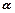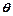|ac+bd|=|coscos+sinsin|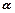            

=|cos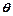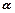（－）|≤1                    

方法二：只需证（ac+bd）²≤（a²+b²）（c²+d²）        

即证：2abcd≤a²d²+b²c²               

即证：（ad－bc）²≥0

上式显然成立

∴原不等式成立。