问题
填空题
关于x的方程|x2-2x|+m+1=0有两个不相等的实数根,则m的取值范围是 ______.
答案
关于x的方程|x2-2x|+m+1=0有两个不相等的实数根,
就是函数y=|x2-2x|与y=-m-1有两个不相同的交点,由图得,当y=-m-1 与x轴重合或在y=1的上方是符合
即-m-1=0 或-m-1>1解得 m=-1 或m<-2
故答案为:m=-1 或m<-2.
关于x的方程|x2-2x|+m+1=0有两个不相等的实数根,则m的取值范围是 ______.
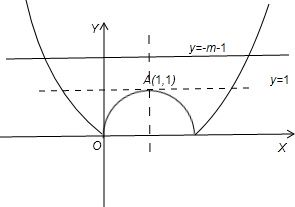
关于x的方程|x2-2x|+m+1=0有两个不相等的实数根,
就是函数y=|x2-2x|与y=-m-1有两个不相同的交点,由图得,当y=-m-1 与x轴重合或在y=1的上方是符合
即-m-1=0 或-m-1>1解得 m=-1 或m<-2
故答案为:m=-1 或m<-2.
