问题
解答题
已知函数f(x)＝|x－1|＋|x－2|.若不等式|a＋b|＋|a－b|≥|a|f(x)(a≠0，a、b∈R)恒成立，求实数x的取值范围．
答案
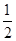≤x≤
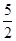
由题知，|x－1|＋|x－2|≤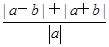
恒成立，故|x－1|＋|x－2|不大于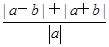的最小值．
∵|a＋b|＋|a－b|≥|a＋b＋a－b|＝2|a|，当且仅当(a＋b)·(a－b)≥0时取等号，
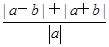∴的最小值等于2.
∴x的范围即为不等式|x－1|＋|x－2|≤2的解，解不等式得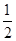≤x≤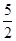.