把A、B两点横坐标分别代入解析式，求出纵坐标，又因为△AOB是直角三角形，可以利用勾股定理列出关于a的方程，求出a的值，便可利用勾股定理求出各边长，进而得出△OAB的周长．

解：如图所示：过点A作AD⊥x轴于D，过点B作BE⊥x轴于E，作AC⊥BE于C．

将x=-1、x=2分别代入解析式得，y_A=a，y_B=4a．

于是BC=4a-a=3a，AC=2-（-1）=3，

所以AB²=（3a）²+3²=9a²+9，

又因为在Rt△ADO中，AO²=a²+1，

在Rt△BOE中，OB²=2²+（4a）²

当∠AOB=90°时，根据勾股定理，AB²=AO²+BO²

即9a²+9=a²+1+2²+（4a）²，解得a=（负值不合题意舍去），

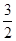于是AO²=+1=，AO=，

OB²=2²+8=12，OB=2，

AB²=AO²+BO²=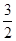+12=，AB=，

△OAB的周长为AO+OB+AB=+2+=2+2，

当∠OAB=90°时，AB²+AO²=BO²，即9a²+9+a²+1=2²+（4a）²，解得a=1，

于是OA=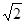，OB=2，AB=3，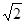

△OAB的周长为AO+OB+AB=4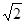+2；

当∠OBA=90°时，AB²=AO²-BO²，即9a²+9=a²+1-[2²+（4a）²]，无解；

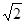∴△OAB的周长为2+2或4+2．

解答此题的关键是作出辅助线，利用勾股定理建立起关于参数a的关系式，再求出各边长，将它们相加即可求出周长．