①当 0≤x＜

1

2

时，

1

2

≤f（x）=x+

1

2

＜1．故当x=

1

4

时，f（x）=

3

4

．

②当

1

2

≤x≤1时，

3

4

≤f（x）=3x²≤3，故当x=

3

3

时，f（x）=1．

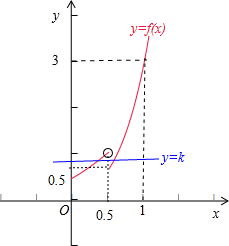
若存在x₁＜x₂，使得f（x₁）=f（x₂）=k，则

1

4

≤x₁ ＜

1

2

≤x₂ ＜1，

如图所示：

显然当k=f（x₁）=f（x₂）=

3

4

时，x₁•f（x₂）取得最小值，

此时，x₁=

1

4

，x₂=

1

2

，x₁•f（x₂）的最小值为

1

4

×

3

4

=

3

16

．

显然，当k=f（x₁）=f（x₂）趋于1时，x₁•f（x₂）趋于最大，

此时，x₁趋于

1

2

，x₂趋于

3

3

，x₁•f（x₂）趋于

1

2

×1=

1

2

．

故x₁•f（x₂）的取值范围为 [

3

16

，

1

2

)，

故选C．