问题
选择题
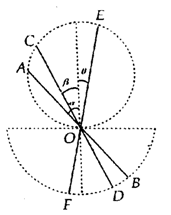
如图所示，在竖直平面内有一半圆，其直径水平且与另一圆的底部相切于O点，O点恰好是下半圆的圆心，现在有三条光滑轨道AB、CD、EF，它们的上下端分别位于上下两圆的圆周上，三轨道都经过切点O，轨道与竖直线的夹角关系为α＞β＞θ，现在让一物块先后从三轨道顶端由静止下滑至底端，则物块在每一条倾斜轨道上滑动时所经历的时间关系为
A．tAB＞tCD＞tEF B．tAB＜tCD＜tEF
C．tAB＝tCD＝tEF， D．无法确定
答案
答案：A
题目分析：设上面圆的半径为R，下面圆的半径为r。分析轨道EF，轨道EF长度为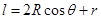
，滑块沿EF下滑的加速度受力分析可知
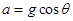，运动时间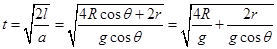
，轨道与竖直方向的夹角越小，时间越短，根据α＞β＞θ判断
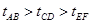,对照选项A对。