问题
解答题
已知实数a、b满足关于x的不等式|x2+ax+b|≤|2x2-4x-16|对一切x∈R恒成立。
（Ⅰ）请验证：a=-2，b=-8满足题意；
（Ⅱ）求出所有满足题意的实数a、b，并说明理由；
（Ⅲ）若对一切x>2均有不等式 x2+ax+b≥(m+2)x-m-15成立，求实数m的取值范围。
答案
解：（Ⅰ）当a=-2，b=-8时，对一切x∈R，
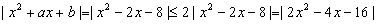恒成立。
（Ⅱ）
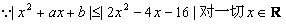恒成立，
∴当x=-2或x=4时成立，此时|2x2-4x-16|=0，
即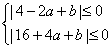
，
得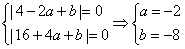
，满足题意的a、b的值仅此一对。
（Ⅲ）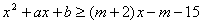
，
即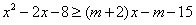
，
即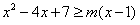
，
∵x>2，
∴
恒成立，
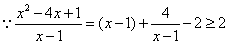（当x=3时，等号成立），
∴m≤2。