问题
解答题
已知函数f(x)=|x-1|+|x+3|.
(1)求x的取值范围,使f(x)为常数函数.
(2)若关于x的不等式f(x)-a≤0有解,求实数a的取值范围.
答案
(1) x∈[-3,1] (2) a≥4
(1)f(x)=|x-1|+|x+3|=
则当x∈[-3,1]时,f(x)为常数函数.
(2)方法一:如图,结合(1)知函数f(x)的最小值为4,
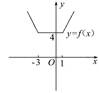
∴实数a的取值范围为a≥4.
方法二:|x-1|+|x+3|≥|x-1-(x+3)|;
∴|x-1|+|x+3|≥4,
等号当且仅当x∈[-3,1]时成立.
得函数f(x)的最小值为4,则实数a的取值范围为a≥4.
