航模兴趣小组设计出一架遥控飞行器，其质量m="2" kg，动力系统提供的恒定升力F＝28 N，试飞时，飞行器从地面由静止开始竖直上升，设飞行器飞行时所受的阻力大小不变，g取10 m/s2.
(1)第一次试飞，飞行器飞行t1＝8 s时到达高度H＝64 m，求飞行器所受阻力Ff的大小；
(2)第二次试飞，飞行器飞行t2＝6 s时遥控器出现故障，飞行器立即失去升力，求飞行器能达到的最大高度h；
(3)为了使飞行器不致坠落到地面，求飞行器从开始下落到恢复升力的最长时间t3.
(1)4 N (2)42 m (3)
s或2.1 s
(1)第一次飞行中，飞行器做匀加速直线运动，设加速度为a1，则有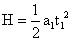
(1分)
由牛顿第二定律可得：F-mg-Ff=ma1 (2分)
解得：Ff＝4 N (1分)
(2)第二次飞行中，设失去升力时的速度为v1，上升的高度为h1，则有：
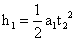(1分)
设失去升力后加速度为a2，上升的高度为h2
由牛顿第二定律可得：mg+Ff＝ma2 (2分)
v1=a1t2 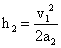(1分)
(1分)
解得：h=h1+h2＝42 m. (1分)
(3)设失去升力下降阶段加速度为a3；恢复升力后加速度为a4；恢复升力时速度为v3，则由牛顿第二定律可得：
mg-Ff=ma3 (2分)
F+Ff-mg=ma4 (1分)
且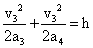
(1分)
v3=a3t3 (1分)
解得：
s(或2.1 s) (1分)