曲线x+1=

1-y2

，即 （x+1）²+y²=1（ x≥-1），

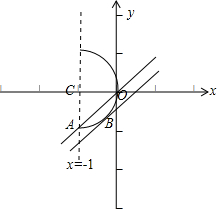
表示以C（-1，0）为圆心，半径等于1的半圆（在直线x-1的右侧），

由题意可得，直线y=x+b与半圆有2个交点．如图所示：

当直线y=x+b过点A（-1，-1）时，把点A的坐标代入可得-1=-1+b，b=0．

当直线y=x+b和半圆相切时，由圆心C（-1，0）到直线y=x+b的距离等于半径可得

|-1-0+b|

2

=1，

解得b=-1+

2

（舍去），或b=-1-

2

．

故b的取值范围是(1-

2

，0]，

故答案为 (1-

2

，0]．