方程

1-x2

x+a

-1=0等价于

1-x2

=x+a．

方程

1-x2

x+a

-1=0仅有一解，即方程

1-x2

=x+a仅有一解，

∴函数y=

1-x2

与函数y=x+a的图象有且只有一个零点．

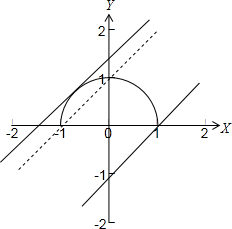
如图所示：

当a=

2

时，直线与半圆相切，满足要求，

当a∈（-1，1]时，直线与半圆相交但只有一个交点，满足要求，

∴实数a的取值范围为{

2

}∪（-1，1]．

故答案为：{

2

}∪（-1，1]．