问题
填空题
请写出一个开口向上,对称轴为直线x=2,且与y轴的交点坐标为(0,3)的抛物线
的解析式 .
答案
y=(x-2)2+3
答案不唯一,如y=x2-4x+3,即y=(x-2)2-1
已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解.顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标.
解:因为开口向上,所以a>0
∵对称轴为直线x=2,
∴-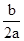 =2
=2
∵y轴的交点坐标为(0,3),
∴c=3.
答案不唯一,如y=x2-4x+3,即y=(x-2)2-1.
