问题
解答题
(2011•广州)已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),且与x轴交于不同的两点A、B,点A的坐标是(1,0)
(1)求c的值;
(2)求a的取值范围;
(3)该二次函数的图象与直线y=1交于C、D两点,设A、B、C、D四点构成的四边形的对角线相交于点P,记△PCD的面积为S1,△PAB的面积为S2,当0<a<1时,求证:S1﹣S2为常数,并求出该常数.
答案
(1)解:把C(0,1)代入抛物线得:0=0+0+c,
解得:c=1,
答:c的值是1.
(2)解:把A(1,0)代入得:0=a+b+1,
∴b=﹣1﹣a,
ax2+bx+1=0,
b2﹣4ac=(﹣1﹣a)2﹣4a=a2﹣2a+1>0,
∴a≠1且a>0,
答:a的取值范围是a≠1且a>0;
(3)证明:∵0<a<1,
∴B在A的右边,
设A(a,0),B(b,0),
∵ax2+(﹣1﹣a)x+1=0,
由根与系数的关系得:a+b=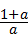 ,ab=
,ab=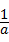 ,
,
∴AB=b﹣a=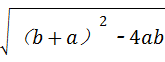 =
=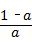 ,
,
把y=1代入抛物线得:ax2+(﹣1﹣a)x+1=1,
解得:x1=0,x2=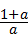 ,
,
∴CD=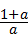 ,
,
过P作MN⊥CD于M,交X轴于N,
则MN⊥X轴,
∵CD∥AB,
∴△CPD∽△BPA,
∴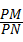 =
=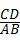 ,
,
∴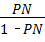 =
=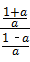 ,
,
∴PN=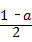 ,PM=
,PM=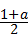 ,
,
∴S1﹣S2=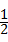 •
•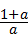 •
•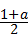 ﹣
﹣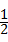 •
•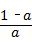 •
•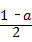 =1,
=1,
即不论a为何只,
S1﹣S2的值都是常数.
答:这个常数是1.
