问题
填空题
当m＝ ▲ 时，抛物线y＝x2－2mx＋4m＋1的顶点位置最高．
答案
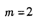
根据二次函数的顶点坐标公式，抛物线y=x2-2mx+4m+1的顶点位置最高，即
取最大值，解答出即可．
解：由题意得，y==
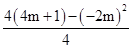=-m2+4m+1=-（m-2）2+5，
抛物线的顶点位置最高，则y=-（m-2）2+5取最大值，
即当m=2时，y=-（m-2）2+5有最大值．
故答案为：2．
点评：本题主要考查了二次函数的最值，确定个二次函数的最值，首先看自变量的取值范围，当自变量取全体实数时，其最值为抛物线顶点坐标的纵坐标；当自变量取某个范围时，要分别求出顶点和函数端点处的函数值，比较这些函数值，从而获得最值．