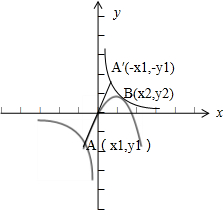问题
选择题
设函数f(x)=
|
答案
当a<0时,作出两个函数的图象,如图,
因为函数f(x)=
是奇函数,所以A与A′关于原点对称,1 x
显然x2>-x1>0,即x1+x2>0,
-y1>y2,即y1+y2<0
故选B.
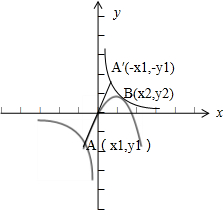
设函数f(x)=
|
当a<0时,作出两个函数的图象,如图,
因为函数f(x)=
是奇函数,所以A与A′关于原点对称,1 x
显然x2>-x1>0,即x1+x2>0,
-y1>y2,即y1+y2<0
故选B.