问题
解答题
已知函数f(x)=x2+2x，g(x)=-x2+2x。
（1）解不等式：g(x)≥f(x)-|x-1|；
（2）若h(x)=g(x)-λf(x)+1在[-1，1]上是增函数，求实数λ的取值范围；
（3）若g(x)≤m2-2mp+1对所有x∈R，p∈[-1，1]恒成立，求实数m的取值范围。
答案
解：（1）g(x)≥f(x)-|x-1|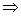
-x2+2x≥x2+2x-|x-1|
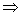-2x2+|x-1|≥0，
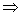
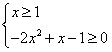或
，
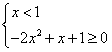解得：x∈[-1，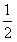
]。
（2）h(x)=g(x)-λf(x)+1=-x2+2x-λ(x2+2x)+1=-(λ+1)x2+2(1-λ)x+1，在[-1，1]单调递增，
①λ+1=0，∴λ=-1时，h(x)=4x+1单调递增；
②λ+1≠0时，对轴称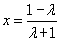
，
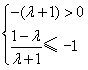
，解得：λ＜-1
或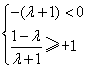
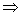
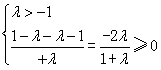，解得：-1＜λ≤0，
∴λ≤0。
（3）g(x)=-x2+2x≤m2-2mp+1，对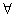
x∈R，p∈[-1，1]恒成立
m2-2mp+1≥(-x2+2x)max=-((x-1)2+1)max=1
m2-2mp≥0，
令f(p)=-2mp+m2，
则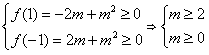
或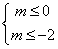
，
∴
。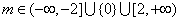