由y=

|x|-1

|x-1|

=

x+1 x-1 (x≤0) -1(0＜x＜1) 1(x＞1)

．

图象如图，

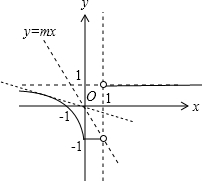
由

y=mx y= x+1 x-1

，得mx²-（m+1）x-1=0．

当m≠0时，由△=[-（m+1）]²+4m=0，解得m=-3-2

2

（舍），或m=-3+2

2

．

由数形结合可知，

满足函数y=mx的图象与函数y=

|x|-1

|x-1|

的图象没有公共点的实数m的取值范围是-1≤m＜-3+2

2

．

故答案为-1≤m＜-3+2

2

．