∵t＞0，关于x的方程程3|x|+

t-4x2

=1

即3|x|-1=-

t-4x2

，-

1

3

≤x≤

1

3

两边 同时平方可得，t-4x²=9x²-6|x|+1

∴t=13x²-6|x|+1

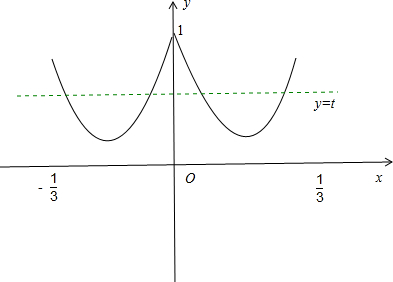
在同一坐标系中画出函数y=13x²-6|x|+1 （-

1

3

≤x≤

1

3

）的图象和函数y=t 的图象如图

①t＜

4

13

或t＞1时，两函数的图象有0个交点

②当t=

4

13

或

4

9

＜t＜1时，两函数的图象有2个交点

③

4

13

＜t＜

4

9

时，两函数的图象有4个交点

④t=1时，两函数的图象有1个交点

∴t＞0，关于x的方程3|x|+

t-4x2

=1有相异实根的个数情况是o或1或2或4

故选B