问题
解答题
已知a，b，c是△ABC的三边，a，b，c满足等式b2=（c+a）（c﹣a），且5b﹣4c=0，求sinA+sinB的值。
答案
解：∵b2=（c+a）（c﹣a），
∴b2=c2﹣a2，即：a2+b2=c2，
∴△ABC是以c为斜边的Rt△ABC，
∵5b﹣4c=0，
∴
，
设b=4k，则c=5k，
∴△ABC中，a=3k，
∴sinA+sinB=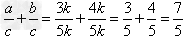
搜题请搜索小程序“爱下问搜题”
已知a，b，c是△ABC的三边，a，b，c满足等式b2=（c+a）（c﹣a），且5b﹣4c=0，求sinA+sinB的值。
解：∵b2=（c+a）（c﹣a），
∴b2=c2﹣a2，即：a2+b2=c2，
∴△ABC是以c为斜边的Rt△ABC，
∵5b﹣4c=0，
∴，
设b=4k，则c=5k，
∴△ABC中，a=3k，
∴sinA+sinB=