问题
解答题
新定义:抛物线在直线的一侧,直线与抛物线有且只有一个公共点时,称直线与抛物线相切;公共点叫做切点。
那么当二次函数y=x2+mx与y=3x+m-2的图象相切时,求:m 的值以及切点的坐标。
答案
答: m 的值为1,切点的坐标为(1,2)
将直线与抛物线联立得到方程: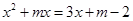 ,
,
整理得: ,
,
由“直线与抛物线有且只有一个公共点时,称直线与抛物线相切”可知该一元二次方程的判别式为0
即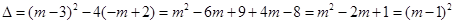 = 0
= 0
所以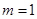 ,把
,把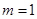 代入方程得到
代入方程得到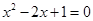 ,解之得:
,解之得: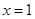 ,
,
把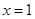 代入
代入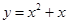 ,得到纵坐标的值
,得到纵坐标的值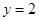
所以切点的坐标(1, 2)
本题的关键思路:构造方程 后,判别式为0
后,判别式为0
