问题
解答题
某渔业公司年初用98万元购买一艘捕鱼船，第一年各种费用12万元，以后每年都增加4万元，每年捕鱼收益50万元。
（1）问第几年开始获利？
（2）若干年后，有两种处理方法：①年平均利润最大时，以26万元出售该船，②总纯收入获利最大时，以8万元出售该渔船，问哪种方案最合算？
答案
解：（1）当50n>98+2n2+10n时公司获利即n2-20n+49＜0
解得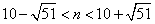
又n∈N+
∴3≤n≤17
因此公司从第3年开始获利。
（2）若按方案①出售：n年的总利润y=50n-（98+2n2+10n）=-2n2+40n-98，则n年的年平均利润
∵
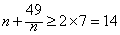
当且仅当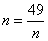
，即n=7时，等号成立
∴当n=7时，年平均利润y1取得最大值为40-2×14=12
按照方案①，7年后，以26万出售该渔船，渔业公司共获利润为12×7+26=110（万元）
若按方案②出售，n年后，总纯收入y2=-2n2+40n-98=-2（n-10）2+102
当n=10时，y2取最大值为102万，此时，再以8万元出售该渔船，渔业公司共获利为：102+8=110（万元）
由于按两种方案出售渔船渔业公司获利相等，但按方案①所需时间少于方案②所需时间，因此，按方案①最合算。
