问题
解答题
已知函数f(x)＝x2＋ax＋b的两个零点是－2和3，解不等式bf(ax)>0；
答案
(－3，2)
由题意，得f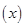
＝(x＋2)(x－3)＝x2－x－6，
所以a＝－1，b＝－6，
所以不等式bf(ax)>0，即为f(－x)<0，即x2＋x－6<0，解得－3<x<2，所以解集为(－3，2)．
搜题请搜索小程序“爱下问搜题”
已知函数f(x)＝x2＋ax＋b的两个零点是－2和3，解不等式bf(ax)>0；
(－3，2)
由题意，得f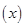＝(x＋2)(x－3)＝x2－x－6，
所以a＝－1，b＝－6，
所以不等式bf(ax)>0，即为f(－x)<0，即x2＋x－6<0，解得－3<x<2，所以解集为(－3，2)．