答案：B

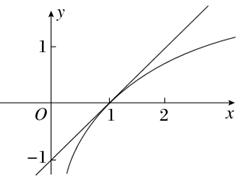
函数f(x)＝lnx－x－a的零点，即为关于x的方程lnx－x－a＝0的实根，将方程lnx－x－a＝0，化为方程lnx＝x＋a，令y₁＝lnx，y₂＝x＋a，由导数知识可知，直线y₂＝x＋a与曲线y₁＝lnx相切时有a＝－1，若关于x的方程lnx－x－a＝0有两个不同的实根，则实数a的取值范围是(－∞，－1)．故选B．