小题1:y=－x²+2x+3

小题2:且x=1时，y有最大值4

小题3:－1≤x≤3

小题4:当n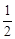＞时，y₁＞y₂；当n=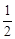，y₁＝y₂；当n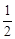＜时，y₁＜y₂

本题考点为二次函数求法以及函数图象开口方向的判断和顶点坐标的求法

小题1:在列表数据中代入两组数据到y=ax²+2x+c中即可求得函数关系式：

如： （-2，-5）代入得    -5="4a-4+c"

（0，3）代入得      3=c           

解联立方程得： a=-1   c=3

故所求二次函数为：y=-x²+2x+3

小题2:由求出的二次函数式y=-x²+2x+3可知，由于二次项系数为-1，所以该函数图象开口向下，故存在最大值。

由二次函数一般形式y=ax²+bx+c的顶点坐标公式可求出x与y的值，即：

  ， 

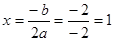小题3:若y≥0，由该函数图象可知，x取值为函数与x轴两交点之间，即：

y=－x²+2x+3

0=－x²+2x+3     

解得x₁=3,x₂=-1，即两交点为：（3，0）与（-1，0）

所以，－1≤x≤3

小题4:由二次函数式y=-x²+2x+3图象可知，必然存在一个n，使得y₁=y₂

设这个n为n₀，则在n₀左侧，函数为上升趋势，在n₀右侧，函数为下降趋势，

即当n＞n₀时y₁＞y₂，当n＜n₀时，y₁＜y₂所以该题关键是求出n₀，即y₁=y₂时n的值

由以上分析可知：-n²+2n+3=-(n+1)²+2(n+1)+3

解方程得 n=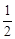

故：当n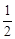＞时，y₁＞y₂；当n=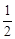，y₁＝y₂；当n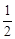＜时，y₁＜y₂