问题
选择题
如图所示,竖直平面内的轨道Ⅰ和Ⅱ都由两段细直杆连接而成,两轨道长度相等。用相同的水平恒力将穿在轨道最低点的B静止小球,分别沿Ⅰ和Ⅱ推至最高点A,所需时间分别为t1、t2;动能增量分别为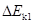 、
、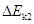 。假定球在经过轨道转折点前后速度的大小不变,且球与Ⅰ、Ⅱ轨道间的动摩擦因数相等,则
。假定球在经过轨道转折点前后速度的大小不变,且球与Ⅰ、Ⅱ轨道间的动摩擦因数相等,则

A.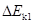 >
>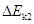 ;t1>t2
;t1>t2
B.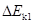 =
=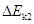 ;t1>t2
;t1>t2
C.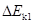 >
>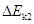 ;t1<t2
;t1<t2
D.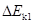 =
=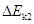 ;t1<t2
;t1<t2
答案
答案:B
题目分析:运动过程包括两个阶段,均为匀加速直线运动。第一个过程和第二个过程运动的位移相等,所以恒力做功相等为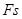 ,高度相等重力做功相等为
,高度相等重力做功相等为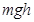 ,设斜面倾角为
,设斜面倾角为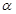 ,斜面长度为
,斜面长度为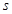 ,则摩擦力做功为
,则摩擦力做功为 ,而
,而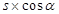 即斜面对应的水平位移,两个过程 的水平位移相等,而
即斜面对应的水平位移,两个过程 的水平位移相等,而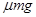 也相等,所以摩擦力做功相等,整理可得合外力做功相等,根据动能定理,合外力做功等于动能变化量,所以动能变化量相等即
也相等,所以摩擦力做功相等,整理可得合外力做功相等,根据动能定理,合外力做功等于动能变化量,所以动能变化量相等即 ,选项AC错。前一个过程加速度先小后大,后一个过程加速度先大后小,做速度时间图像如下,既要末速度相同,又要位移相同,即末速度相同,与时间轴围成的面积相等,根据图像可判断
,选项AC错。前一个过程加速度先小后大,后一个过程加速度先大后小,做速度时间图像如下,既要末速度相同,又要位移相同,即末速度相同,与时间轴围成的面积相等,根据图像可判断 ,对照选项B对。
,对照选项B对。

