问题
填空题
关于x的方程x3－3x2－a＝0有三个不同的实数解，则实数a的取值范围是________．
答案
(－4,0)
由题意知使函数f(x)＝x3－3x2－a的极大值大于0且极小值小于0即可，又f′(x)＝3x2－6x＝3x(x－2)，令f′(x)＝0，得x1＝0，x2＝2.当x＜0时，f′(x)＞0；当0＜x＜2时，f′(x)＜0；当x＞2时，f′(x)＞0，所以当x＝0时，f(x)取得极大值，即f(x)极大值＝f(0)＝－a；当x＝2时，f(x)取得极小值，即f(x)极小值＝f(2)＝－4－a，所以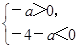
解得－4＜a＜0.，