问题
解答题
已知不等式（ax﹣1）（x+1）＜0 （a∈R）．
（1）若x=a时不等式成立，求a的取值范围；
（2）当a≠0时，解这个关于x的不等式．
答案
解：（1）由x=a时不等式成立，即（a2﹣1）（a+1）＜0，
所以（a+1）2（a﹣1）＜0，所以a＜1且a≠﹣1．
所以a的取值范围为（﹣∞，﹣1）∪（﹣1，1）．
（2）当a＞0时，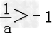
，所以不等式的解：
；
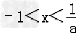当﹣1＜a＜0时，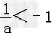
，所以不等式的解：
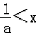或x＞﹣1；
当a＜﹣1时，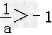
，所以不等式的解：x＜﹣1或
．
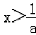综上：当a＞0时，所以不等式的解：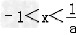
；
当﹣1＜a＜0时，所以不等式的解：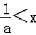
或x＞﹣1；
当a＜﹣1时，所以不等式的解：x＜﹣1或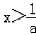
．