问题
解答题
已知二次函数f(x)＝x2＋2bx＋c(b、c∈R)．
(1)若f(x)≤0的解集为{x|－1≤x≤1}，求实数b、c的值；
(2)若f(x)满足f(1)＝0，且关于x的方程f(x)＋x＋b＝0的两个实数根分别在区间(－3，－2)，(0,1)内，求实数b的取值范围．
答案
（1）b＝0，c＝－1
（2）
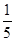<b<
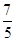
解：(1)依题意，x1＝－1，x2＝1是方程x2＋2bx＋c＝0的两个根．
由韦达定理，得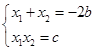
即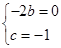
所以b＝0，c＝－1．
(2)由题知，f(1)＝1＋2b＋c＝0，所以c＝－1－2b．
记g(x)＝f(x)＋x＋b＝x2＋(2b＋1)x＋b＋c＝x2＋(2b＋1)x－b－1，
则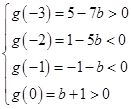
，
解得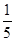<b<，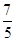
所以实数b的取值范围为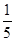<b<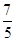．