问题
计算题
解关于x的不等式x2﹣(a2+a)x+a3>0(a为参数).
答案
解:x2﹣(a2+a)x+a3>0, 因式分解得:(x﹣a)(x﹣a2)>0,
若a>a2,则a2﹣a<0,即0<a<1时,
原不等式可化为: 或
或 ,
,
解得:x>a或x<a2,
此时原不等式的解集为{x|x<a2或x>a};
若a<a2,即a<0或a>1时,原不等式可化为: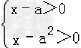 或
或 ,
,
解得:x<a或x>a2,
此时原不等式的解集为{x|x<a或x>a2};
若a=a2,即a=0或a=1时,原不等式化为:(x﹣a)2>0,
∴x≠0且x≠1,此时原不等式的解集为{x∈R|x≠0且x≠1},
则当0≤a≤1时,原不等式的解集为{x|x<a2或x>a};
当a<0或a>1时,原不等式的解集为{x|x<a或x>a2}.