当m为何值时,方程x2-4|x|+5-m=0有四个不相等的实数根?
1<m<5
方程x2-4|x|+5-m=0变形为x2-4|x|+5=m,
设y1=x2-4|x|+5=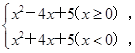
y2=m,在同一坐标系下分别作出函数y1和y2的图象,如图所示.
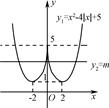
由两个函数图象的交点可以知道,当两函数图象有四个不同交点,即方程有四个不同的实数根,满足条件的m取值范围是1<m<5.
当m为何值时,方程x2-4|x|+5-m=0有四个不相等的实数根?
1<m<5
方程x2-4|x|+5-m=0变形为x2-4|x|+5=m,
设y1=x2-4|x|+5=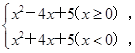
y2=m,在同一坐标系下分别作出函数y1和y2的图象,如图所示.

由两个函数图象的交点可以知道,当两函数图象有四个不同交点,即方程有四个不同的实数根,满足条件的m取值范围是1<m<5.