问题
选择题
设函数f(x)＝ln x，g(x)＝x2－4x＋4，则方程f(x)－g(x)＝0的实根个数是 ( )．
A．0
B．1
C．2
D．3
答案
答案：C
由f(x)－g(x)＝0，得f(x)＝g(x)．
在同一坐标系内作出函数y＝f(x)与y＝g(x)的图象，
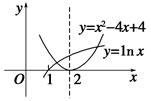
由图知f(x)，g(x)的图象有两个交点．
因此方程f(x)－g(x)＝0有两个不相等的实根．
搜题请搜索小程序“爱下问搜题”
设函数f(x)＝ln x，g(x)＝x2－4x＋4，则方程f(x)－g(x)＝0的实根个数是 ( )．
A．0
B．1
C．2
D．3
答案：C
由f(x)－g(x)＝0，得f(x)＝g(x)．
在同一坐标系内作出函数y＝f(x)与y＝g(x)的图象，
由图知f(x)，g(x)的图象有两个交点．
因此方程f(x)－g(x)＝0有两个不相等的实根．
