问题
解答题
已知函数f（x）=x2+ax+6．
（1）当a=5时，解不等式f（x）＜0；
（2）若不等式f（x）＞0的解集为R，求实数a的取值范围．
答案
解：（1）∵当a=5时，不等式f（x）＜0
即 x2+5x+6＜0，
∴（x+2）（x+3）＜0，
∴﹣3＜x＜﹣2．
∴不等式f（x）＜0的解集为{x|﹣3＜x＜﹣2}
（2）不等式f（x）＞0的解集为R，
∴x的一元二次不等式x2+ax+6＞0的解集为R，
∴△=a2﹣4×6＜0
∴﹣2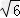
＜a＜2
∴实数a的取值范围是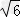（﹣2
，2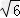
）