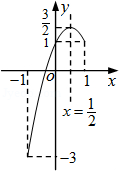问题
解答题
已知：y关于x的函数y=（k﹣1）x2﹣2kx+k+2的图象与x轴有交点．
（1）求k的取值范围；
（2）若x1，x2是函数图象与x轴两个交点的横坐标，且满足（k﹣1）x12+2kx2+k+2=4x1x2．
①求k的值；②当k≤x≤k+2时，请结合函数图象确定y的最大值和最大值．
答案
（1）k的取值范围是k≤2
（2）①k值为﹣1②y的最大值为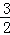
，最小值为﹣3
（1）当k=1时，函数为一次函数y=﹣2x+3，其图象与x轴有一个交点．…（1分）
当k≠1时，函数为二次函数，其图象与x轴有一个或两个交点，
令y=0得（k﹣1）x2﹣2kx+k+2=0．
△=（﹣2k）2﹣4（k﹣1）（k+2）≥0，解得k≤2．即k≤2且k=1．…（2分）
综上所述，k的取值范围是k≤2．…（3分）
（2）①∵x1≠x2，由（1）知k＜2且k=1．
由题意得（k﹣1）x12+（k+2）=2kx1．（*）…（4分）
将（*）代入（k﹣1）x12+2kx2+k+2=4x1x2中得：
2k（x1+x2）=4x1x2．…（5分）
又∵x1+x2=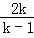
，x1x2=
，
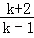∴2k•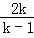=4•
．…（6分）
解得：k1=﹣1，k2=2（不合题意，舍去）．
∴所求k值为﹣1．…（7分）
②如图，∵k1=﹣1，y=﹣2x2+2x+1=﹣2（x﹣
）2+．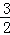
且﹣1≤x≤1．…（8分）
由图象知：当x=﹣1时，y最小=﹣3；当x=时，y最大=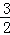．…（9分）
∴y的最大值为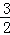，最小值为﹣3．…（10分）
