问题
选择题
若函数f(x)=|4x-x2|-a的零点个数为4，则a的取值范围是（ ）
A．[0,3]
B．(0，4）
C．[-1,2]
D．(-1,4)
答案
答案：B
函数f(x)=|4x-x2|-a的零点个数为4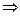
方程|4x-x2|-a=0有4个不同的根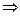a=|4x-x2|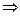函数g(x)=a与函数F(x)=|4x-x2|的图象有4个不同的交点
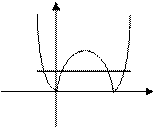
作出4x-x2的图象,可知在x=2处其有最大值4
∴若直线g(x)=a与函数F(x)=|4x-x2|的图象有4个不同的交点,则a∈(0,4)