问题
解答题
某政府大力扶持大学生创业．李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯．物价部门规定，这种护眼台灯的销售单价不得高于32元．销售过程中发现，月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=－10x＋n．
（1）当销售单价x定为25元时，李明每月获得利润为w为1250元，则n= ；
（2）如果李明想要每月获得2000元的利润，那么销售单价应定为多少元？
（3）当销售单价定为多少元时，每月可获得最大利润？并求最大利润为多少元．
答案
（1）500，（2）30元（3）销售单价定为32元时，每月可获得最大利润，最大利润为2160元
（1）500……………………………………………2分
（2）由题意，得：w = (x－20)·y……………………………………………………3分
=(x－20)·(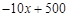
)
………………………………………4分
令：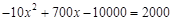
……………………………………………5分
解这个方程得：x1 = 30，x2 = 40（舍）．
答：李明想要每月获得2000元的利润，销售单价应定为30元. …………6分
（3）由（2）知：w ∴
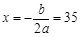.…………………7分
∵－10＜0，∴抛物线开口向下.
∵x≤32 ∴w随x的增大而减小.………………………………8分
∴当x =32时，w最小＝2160.…………………………………………9分
答：销售单价定为32元时，每月可获得最大利润，最大利润为2160元…10分
（1）把已知量代入一次函数中得出n的值；
（2）利用利润=单位利润×数量列出方程，然后解出方程；
（3）同（2）相同，根据抛物线的性质得出最大利润。