问题
解答题
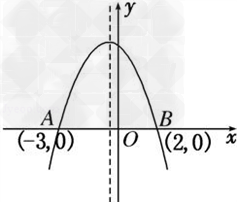
已知函数f（x）=ax2+（b﹣8）x﹣a﹣ab（a≠0），当x∈（﹣3，2）时，f（x）＞0；当
x∈（﹣∞，﹣3）∪（2，+∞）时，f（x）＜0．
（1）求f（x）在[0，1]内的值域；
（2）c为何值时，不等式ax2+bx+c≤0在[1，4]上恒成立．
答案
解：由题意得x=﹣3和x=2是函数f（x）的零点且a≠0，
则
解得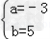
∴f（x）=﹣3x2﹣3x+18．
（1）由图象知，函数在[0，1]内单调递减，
∴当x=0时，y=18；当x=1时，y=12，
∴f（x）在[0，1]内的值域为[12，18]．
（2）令g（x）=﹣3x2+5x+C、
∵g（x）在[
，+∞）上单调递减，要使g（x）≤0在[1，4]上恒成立，
则需要g（1）≤0．即﹣3+5+c≤0，
解得c≤﹣2，
∴当c≤﹣2时，不等式ax2+bx+c≤0在[1，4]上恒成立．
