问题
计算题
设函数y＝kx2＋(2k＋1)x＋1(k为实数)．
小题1:写出其中的两个特殊函数，使它们的图象不全是抛物线，并在同一直角坐标系中用描点法画出这两个特殊函数的图象
小题2:根据所画图象，猜想出：对任意实数k，函数的图象都具有的特征，并给予证明
小题3:对任意负实数k，当x<m时，y随着x的增大而增大，试求出m的一个值
答案
小题1:当k=1时，y= x2＋3x+1;当k=0时y="x+1," 图象略
小题2:见解析
小题3:只要m的值不大于-1即可
（1）当k=1时，y= x2＋3x+1;当k=0时y="x+1," 图象略
(2) 对任意实数k, 函数的图象都经过点（-2，-1）和点（0,1）
证明；把x=-2代入函数y＝kx2＋(2k＋1)x＋1，得y=-1，即函数y＝kx2＋(2k＋1)x＋1的图像经过点（-2，-1）；把x=0代入函数y＝kx2＋(2k＋1)x＋1，得y=1，即函数y＝kx2＋(2k＋1)x＋1的图像经过点（0,1）
（3）当k为任意负实数，该函数的图像总是开口向下的抛物线，其对称轴为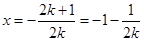
，当负数k所取的值非常小时，正数
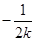靠近0，所以
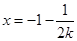靠近-1，所以只要m的值不大于-1即可。