问题
解答题
某商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件。设这种商品的销售单价为x元,商品每天销售这种商品所获得的利润为y元. (1)给定x的一些值,请计算y的一些值.(每空1分,共4分)
(3)请探索:当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?这时每天销售的商品是多少件?(4分)
|
答案
(1)如表。
(2)解: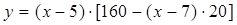

由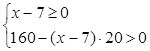 ,得
,得 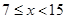
(直接写出自变量x的取值范围的也给分)
答:y与x之间的函数关系式为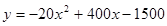 ,
,
自变量x的取值范围是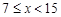 。
。
(3)
∵  ,
,
∴ 当x =10时,y有最大值500.
当x =10时,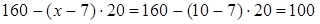
答:当商品的销售单价定为10元时,该商店销售这种商品获得的利润最大,最大利润为500元,这时每天销售的商品是100件.
(1)根据等量关系“利润=每件的利润×每天售出的件数”得出单价依次上涨时获得的利润.
(2)根据“利润值=(销售单价-购进单价)×{160-20(销售单价-7)}”,列出一元二次方程.然后根据销售差价不能小于零,且销售产品量大于零,从而求出自变量x的取值范围;
(3)利用(2)得出的函数关系式,将自变量配成完全平方式,然后再根据一元二次方程函数图象求出它的最大值.
