问题
问答题
已知函数z=f(x，y)的全微分dz=2xdx-2ydy，并且f(1，1)=2．求f(x，y)在椭圆域D=(x，y)|x2+
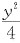≤1上的最大值和最小值．
答案
参考答案：(1) 求f(x，y)的表达式．
由已知有dx=dx2-dy2=d(x2-y2)[*]z=x2-y2+C．
又因为f(1．1)=2，所以C=2，从而z=f(x，y)=x2-y2+2．
(2) 求f(x，y)在D内驻点及相应函数值．
解
[*]
得(x，y)=(0，0)，即f(x，y)在D内有唯一驻点(0，0)，且f(0，0)=2．
(3) 求f(x，y)在D的边界y2=4(1-x2)上的最大值和最小值．将y2=4(1-x2)(|x|≤1)代入z=x2-y2+2，得
z(x)=x2-4(1-x2)+2=5x2-2．
显然，z(x)在[-1，1]上的最大值为3，最小值为-2．
综上所述，z=f(x，y)在D上的最大值是max{2，3，-2}=3，最小值是min{2，3，-2