问题
解答题
已知抛物线y=ax2+4ax+m(a≠0)与x轴的交点为A(-1,0),B(x2,0)。
(1)直接写出一元二次方程ax2+4ax+m=0的两个根:x1 = , x2 =
(2)原抛物线与y轴交于C点,CD∥x轴交抛物线于D点,求CD的值;
(3)若点E(1,y1),点F(-3,y2)在原抛物线上,你能比较出y2和y1; 的大小吗?若能,请比较出大小,若不能,请说明理由。
答案
解:(1)x1 = -1 , x2 = -3
(2)∵抛物线y=ax2+4ax+m的对称轴是x=-2,点C是抛物线y=ax2+4ax+m与y轴的交点,
∴C到对称轴的距离是2,又∵CD∥x轴 ∴CD的距离是点C到对称轴距离的2倍,即2×2=4 即CD的值为4。
(3)不能判断出y2和y1; 的大小。因为抛物线y=ax2+4ax+m中a的正、负不能确定,也就不能确定抛物线的开口方向,抛物线是上升还是下降也就不能确定,因此y值随x值的变化也不能确定,所以不能判断出y2和y1; 的大小。
(1)先计算出抛物线的对称轴,再根据抛物线的对称性即可得到结果;
(2)根据抛物线的对称轴即可求出C到对称轴的距离,再根据抛物线的对称性即可得到结果;
(3)因为抛物线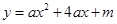 中a的正、负不能确定,也就不能确定抛物线的开口方向,抛物线是上升还是下降也就不能确定,因此y值随x值的变化也不能确定,所以不能判断出
中a的正、负不能确定,也就不能确定抛物线的开口方向,抛物线是上升还是下降也就不能确定,因此y值随x值的变化也不能确定,所以不能判断出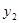 和
和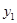 的大小。
的大小。
