问题
解答题
有一种产品的质量分成6种不同档次,若工时不变,每天可生产最低档次的产品40件;如果每提高一个档次,每件利润可增加1元,但每天要少生产2件产品。
⑴若最低档次的产品每件利润17元时,生产哪一种档次的产品的利润最大?并求最大利润。
⑵由于市场价格浮动,生产最低档次的产品每件利润可以从8元到24元不等,那么生产哪种档次的产品所得利润最大?
答案
解:⑴设生产第X档次的产品,获得利润为y元,则
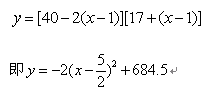
∴当X=2.5时,y的最大值为684.5
∵x为正整数
∴x=2时,y=684,x=3时,y=684,
∴当生产第2档次或第3档次的产品时所获得利润最,最大利润为684元
⑵设生产最低档次的产品每件利润为a元,生产第x档次的产品,获得利润为y元,则

(1)先确定生产第x档次的产品,再表示出利润y的函数关系式,利用配方法求出最大利润;
(2)设生产最低档次的产品每件利润为a元,再表示出利润y的函数关系式,由x与a的关系可得x的值,再根据函数最值即可求得结果。
