问题
解答题
函数f(x)=x2+ax+3.
(1)当x∈R时,f(x)≥a恒成立,求a的取值范围.
(2)当x∈[-2,2]时,f(x)≥a恒成立,求a的取值范围.
答案
(1)∵x∈R时,有x2+ax+3-a≥0恒成立,
须△=a2-4(3-a)≤0,即a2+4a-12≤0,所以-6≤a≤2.
(2)当x∈[-2,2]时,设g(x)=x2+ax+3-a≥0,
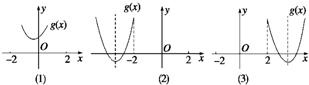
分如下三种情况讨论(如图所示):
①如图(1),当g(x)的图象恒在x轴上方时,满足条件时,有△=a2-4(3-a)≤0,即-6≤a≤2.
②如图(2),g(x)的图象与x轴有交点,
但在x∈[-2,+∞)时,g(x)≥0,即
即△≥0 x=-
≤-2a 2 g(-2)≥0
⇔a2-4(3-a)≥0 -
≤-2a 2 4-2a+3-a≥0
解之得a∈Φ.a≥2或a≤-6 a≥4 a≤ 7 3
③如图(3),g(x)的图象与x轴有交点,
但在x∈(-∞,2]时,g(x)≥0,即
即△≥0 x=-
≥2a 2 g(2)≥0
⇔a2-4(3-a)≥0 -
≥2a 2 4+2a+3-a≥0
⇔-7≤a≤-6a≥2或a≤-6 a≤-4 a≥-7
综合①②③得a∈[-7,2].
