问题
解答题
某大学对在校的学生进行素质拓展测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为
(Ⅰ)求该小组中女生的人数; (Ⅱ)若从中随机选3人参加测试,求所选的三人恰为两名男生一名女生的概率; (Ⅲ)假设此项测试对该小组的学生而言,每个女生通过的概率均为
|
答案
(Ⅰ)设该小组中有n个女生,
由题意,得
=C 1n C 110-n C 210
,…(2分)8 15
解得n=6或n=4(舍),
所以该小组有6名女生.…(4分)
(Ⅱ)恰为两名男生一名女生的概率P=
=C 24 C 16 C 310
…(7分)3 10
(Ⅲ)由题意,ξ的取值为0,1,2,3,
P(ξ=0)=
×1 3
×1 3
=1 4
,1 36
P(ξ=1)=C
× 12
×2 3
×1 3
+(1 4
)2×1 3
=3 4
,7 36
P(ξ=2)=×
×2 3
×1 3
+(3 4
)2×1 3
=1 4
,16 36
P(ξ=3)=(
)2×2 3
=3 4
.…(11分)12 36
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 36 |
| 7 |
| 36 |
| 16 |
| 36 |
| 12 |
| 36 |
| 25 |
| 12 |

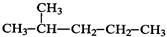 和
和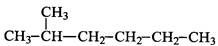
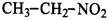 和
和
 和
和