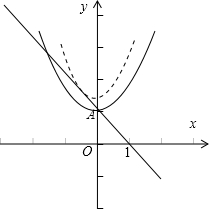
在同一坐标系画出函数y=|x-1|和 y=

1

2

x2-a 的图象，

当y=|x-1|过点（0，-a）时，-a=|0-1|=1，∴a=-1．

当y=

1

2

x2-a 和直线y=-x+1相切时，-x+1=

1

2

x2-a，即x²+2x-2a-2=0，

由判别式△=4-4（-2a-2）=0，解得a=-

3

2

．

数形结合可得实数a的取值范围是 （-

3

2

，-1]，

故答案为 （-

3

2

，-1]．